Decade
Leetcode 383场周赛
Zhongjun Qiu 元婴开发者
  2024-02-04 15:21:08   2025-04-29 21:27:59    2.4k Words  10 Mins  

Q1 100214. 边界上的蚂蚁 [Easy] 题解

Q2 100189. 找出网格的区域平均强度 [Medium] 题解

Q3 100203. 将单词恢复初始状态所需的最短时间 [Hard] 题解

100214. 边界上的蚂蚁

边界上有一只蚂蚁，它有时向 左 走，有时向 右 走。

给你一个 非零 整数数组 nums 。蚂蚁会按顺序读取 nums 中的元素，从第一个元素开始直到结束。每一步，蚂蚁会根据当前元素的值移动：

  • 如果 nums[i] < 0 ，向 左 移动 -nums[i]单位。
  • 如果 nums[i] > 0 ，向 右 移动 nums[i]单位。

返回蚂蚁 返回 到边界上的次数。

注意：

  • 边界两侧有无限的空间。
  • 只有在蚂蚁移动了 |nums[i]| 单位后才检查它是否位于边界上。换句话说，如果蚂蚁只是在移动过程中穿过了边界，则不会计算在内。

示例 1：

1
2
3
4
5
6
输入：nums = [2,3,-5]
输出：1
解释：第 1 步后，蚂蚁距边界右侧 2 单位远。
第 2 步后，蚂蚁距边界右侧 5 单位远。
第 3 步后，蚂蚁位于边界上。
所以答案是 1 。

示例 2：

1
2
3
4
5
6
7
输入：nums = [3,2,-3,-4]
输出：0
解释：第 1 步后，蚂蚁距边界右侧 3 单位远。
第 2 步后，蚂蚁距边界右侧 5 单位远。
第 3 步后，蚂蚁距边界右侧 2 单位远。
第 4 步后，蚂蚁距边界左侧 2 单位远。
蚂蚁从未返回到边界上，所以答案是 0 。

提示：

  • 1 <= nums.length <= 100
  • -10 <= nums[i] <= 10
  • nums[i] != 0

思路

​ 模拟一下即可。

代码

1
2
3
4
5
6
7
8
9
10
function returnToBoundaryCount(nums: number[]): number {
    let ans = 0, sum = 0;
    nums.forEach(v => {
        sum += v;
        if (sum == 0){
            ans++;
        }
    });
    return ans;
};

复杂度分析

  • 时间：O(n)。
  • 空间：O(1)。

100189. 找出网格的区域平均强度

给你一个下标从 0 开始、大小为 m x n 的网格 image ，表示一个灰度图像，其中 image[i][j] 表示在范围 [0..255] 内的某个像素强度。另给你一个 非负 整数 threshold 。

如果 image[a][b] 和 image[c][d] 满足 |a - c| + |b - d| == 1 ，则称这两个像素是 相邻像素 。

区域 是一个 3 x 3 的子网格，且满足区域中任意两个 相邻 像素之间，像素强度的 绝对差 小于或等于 threshold 。

区域 内的所有像素都认为属于该区域，而一个像素 可以 属于 多个 区域。

你需要计算一个下标从 0 开始、大小为 m x n 的网格 result ，其中 result[i][j] 是 image[i][j] 所属区域的 平均 强度，向下取整 到最接近的整数。如果 image[i][j] 属于多个区域，result[i][j] 是这些区域的 “取整后的平均强度” 的 平均值，也 向下取整 到最接近的整数。如果 image[i][j] 不属于任何区域，则 result[i][j] 等于 image[i][j] 。

返回网格 result 。

示例 1：

img 
1
2
3
4
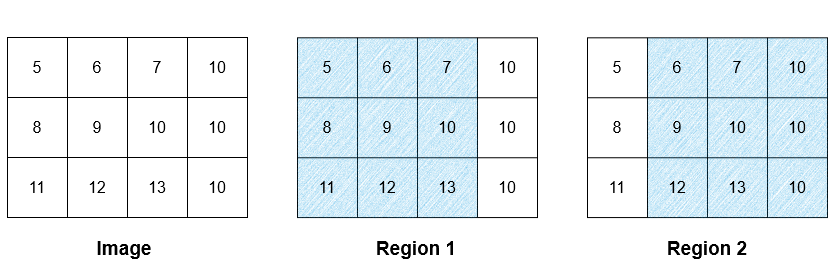
输入：image = [[5,6,7,10],[8,9,10,10],[11,12,13,10]], threshold = 3
输出：[[9,9,9,9],[9,9,9,9],[9,9,9,9]]
解释：图像中存在两个区域，如图片中的阴影区域所示。第一个区域的平均强度为 9 ，而第二个区域的平均强度为 9.67 ，向下取整为 9 。两个区域的平均强度为 (9 + 9) / 2 = 9 。由于所有像素都属于区域 1 、区域 2 或两者，因此 result 中每个像素的强度都为 9 。
注意，在计算多个区域的平均值时使用了向下取整的值，因此使用区域 2 的平均强度 9 来进行计算，而不是 9.67 。

示例 2：

img 
1
2
3
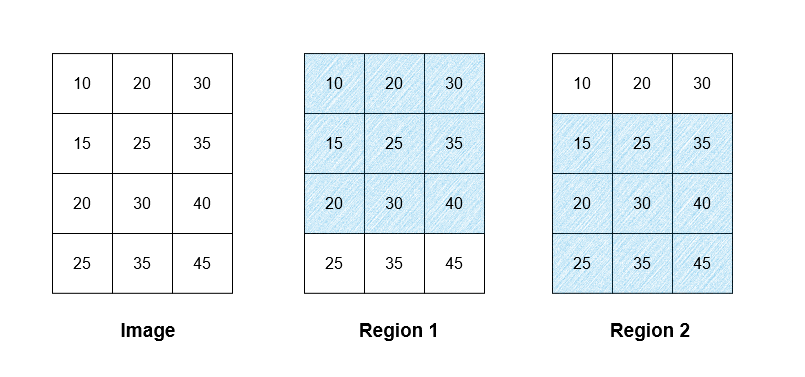
输入：image = [[10,20,30],[15,25,35],[20,30,40],[25,35,45]], threshold = 12
输出：[[25,25,25],[27,27,27],[27,27,27],[30,30,30]]
解释：图像中存在两个区域，如图片中的阴影区域所示。第一个区域的平均强度为 25 ，而第二个区域的平均强度为 30 。两个区域的平均强度为 (25 + 30) / 2 = 27.5 ，向下取整为 27 。图像中第 0 行的所有像素属于区域 1 ，因此 result 中第 0 行的所有像素为 25 。同理，result 中第 3 行的所有像素为 30 。图像中第 1 行和第 2 行的像素属于区域 1 和区域 2 ，因此它们在 result 中的值为 27 。

示例 3：

1
2
3
输入：image = [[5,6,7],[8,9,10],[11,12,13]], threshold = 1
输出：[[5,6,7],[8,9,10],[11,12,13]]
解释：图像中不存在任何区域，因此对于所有像素，result[i][j] == image[i][j] 。

提示：

  • 3 <= n, m <= 500
  • 0 <= image[i][j] <= 255
  • 0 <= threshold <= 255

思路

​ 阅读理解题。

  1. 遍历每一个3X3方格。
  2. 维护一个dp数组：dp(i)(j)[0]表示该像素所属区域强度和，dp(i)(j)[1]表示该像素总共属于多少个区域。
  3. 判断该方格是否为一个区域：即判断相邻格子像素差是否小于threshold
  4. 如果是区域：则再次遍历区域中每一个像素，维护dp数组值。
  5. 最后dp(i)(j)[0]/dp(i)(j)[1]则是每个像素所属区域强度和的均值；
  6. 如果dp(i)(j)[0]等于0，说明像素不属于任何一个区域，答案是它自己像素值。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    vector<vector<int>> resultGrid(vector<vector<int>>& image, int threshold) {
        int n = image.size(), m = image[0].size();
        vector<vector<int>> ans(n, vector<int>(m, 0));
        vector<vector<vector<int>>> dp(n, vector<vector<int>>(m, vector<int>(2, 0)));
        for (int i = 0;i <= n-3;i++){
            for (int j = 0;j <= m-3;j++){
                int flag = 1, sum = 0;
                for (int k = 0;k < 3 && flag==1;k++){
                    for (int l = 0;l < 3 && flag==1;l++){
                        int cur = image[i+k][j+l];
                        sum += cur;
                        int left = l==2?cur:image[i+k][j+l+1];
                        int down = k==2?cur:image[i+k+1][j+l];
                        if (abs(cur-left) > threshold || abs(cur-down) > threshold){
                            flag = 0;
                        }
                    }
                }
                if (flag == 1){
                    for (int k = 0;k < 3;k++){
                        for (int l = 0;l < 3;l++){
                            dp[i+k][j+l][0] += sum/9;
                            dp[i+k][j+l][1]++;
                        }
                    }
                }
            }
        }
        for (int i = 0;i < n;i++){
            for (int j = 0;j < m;j++){
                if (dp[i][j][1] > 0){
                    ans[i][j] = dp[i][j][0]/dp[i][j][1];
                }else{
                    ans[i][j] = image[i][j];
                }
            }
        }
        return ans;
    }
};

复杂度分析

  • 时间：O(n*m*9)。
  • 空间：O(n*m)。

100203. 将单词恢复初始状态所需的最短时间

给你一个下标从 0 开始的字符串 word 和一个整数 k 。

在每一秒，你必须执行以下操作：

  • 移除 word 的前 k 个字符。
  • 在 word 的末尾添加 k 个任意字符。

注意 添加的字符不必和移除的字符相同。但是，必须在每一秒钟都执行 两种 操作。

返回将 word 恢复到其 初始 状态所需的 最短 时间（该时间必须大于零）。

示例 1：

1
2
3
4
5
6
输入：word = "abacaba", k = 3
输出：2
解释：
第 1 秒，移除 word 的前缀 "aba"，并在末尾添加 "bac" 。因此，word 变为 "cababac"。
第 2 秒，移除 word 的前缀 "cab"，并在末尾添加 "aba" 。因此，word 变为 "abacaba" 并恢复到始状态。
可以证明，2 秒是 word 恢复到其初始状态所需的最短时间。

示例 2：

1
2
3
4
5
输入：word = "abacaba", k = 4
输出：1
解释：
第 1 秒，移除 word 的前缀 "abac"，并在末尾添加 "caba" 。因此，word 变为 "abacaba" 并恢复到初始状态。
可以证明，1 秒是 word 恢复到其初始状态所需的最短时间。

示例 3：

1
2
3
4
5
6
输入：word = "abcbabcd", k = 2
输出：4
解释：
每一秒，我们都移除 word 的前 2 个字符，并在 word 末尾添加相同的字符。
4 秒后，word 变为 "abcbabcd" 并恢复到初始状态。
可以证明，4 秒是 word 恢复到其初始状态所需的最短时间。

提示：

  • 1 <= word.length <= 10^5
  • 1 <= k <= word.length
  • word仅由小写英文字母组成。

思路

  1. 由于可以往s的末尾添加任意字符，这意味着只要s[k:]是s的前缀，就能让s恢复成其初始值，其中s[k:]表示从s[k]开始的后缀。

  2. 即需要找到最小的t，使得s[tk:]是s的前缀。

    1
    2
    3
    s = abacaba，k = 4 时
    第一秒后，s[4:]=aba，是s的前缀。
    相当于最前面删除abac，最后面加上caba。

    1
    2
    3
    4
    s = abacaba，k = 3 时
    第一秒后，s[3:]=caba，不是s的前缀。
    第二秒后，s[6:]=a，是s的前缀。
    相当于最前面删除aba和cab，最后面加上bac和aba。

  3. 判断前后缀一般有两种方法：

    • KMP
    • 字符串哈希

代码

KMP

next[i]表示最长相同前后缀的长度。

例如：next(s = abacaba) = [0,0,1,0,1,2,3]，k = 3。

一开始相同前后缀长度 len = next[n-1] = 3。(此时前后缀为aba)。

但需要删除abac四个字符，不是k的整数倍。再次寻找次短相同前后缀长度。

len = next[len-1] = next[2] = 1。（此时前后缀为a）。

需要删除abacab六个字符，是k的两倍，符合题意。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    // 基础的KMP计算next数组
    vector<int> calcLSP(string s){
        int n = s.size();
        vector<int> next(n, 0);
        for (int i = 1, j = 0;i < n;i++){
            while (j && s[i] != s[j]) j = next[j - 1];
            if (s[i] == s[j]) j++;
            next[i] = j;
        }
        return next;
    }
    int minimumTimeToInitialState(string word, int k){
        int n = word.size();
        vector<int> next = calcLSP(word);
        for (int len = next[n-1];;){
            // 枚举每一个可能的相同前后缀长度
            if ((n-len)%k == 0) return (n-len+k-1)/k;
            // 下一个相同前后缀长度（肯定比现在长度小）
            len = next[len-1];
        }
        return (n+k-1)/k;
    }
};
  • 时间：O(n)。
  • 空间：O(n)。
Leetcode 383场周赛
2024/02/04/Leetcode-383场周赛/
Author
Zhongjun Qiu
Published
2024-02-04 15:21
License
 REWARD AUTHOR
 Comments
Comment plugin failed to load
Loading comment plugin
  1. 100214. 边界上的蚂蚁
    1. 思路
    2. 代码
    3. 复杂度分析
  2. 100189. 找出网格的区域平均强度
    1. 思路
    2. 代码
    3. 复杂度分析
  3. 100203. 将单词恢复初始状态所需的最短时间
    1. 思路
    2. 代码
      1. KMP
  1. 100214. 边界上的蚂蚁
    1. 思路
    2. 代码
    3. 复杂度分析
  2. 100189. 找出网格的区域平均强度
    1. 思路
    2. 代码
    3. 复杂度分析
  3. 100203. 将单词恢复初始状态所需的最短时间
    1. 思路
    2. 代码
      1. KMP